Muon basics
The origin of muons
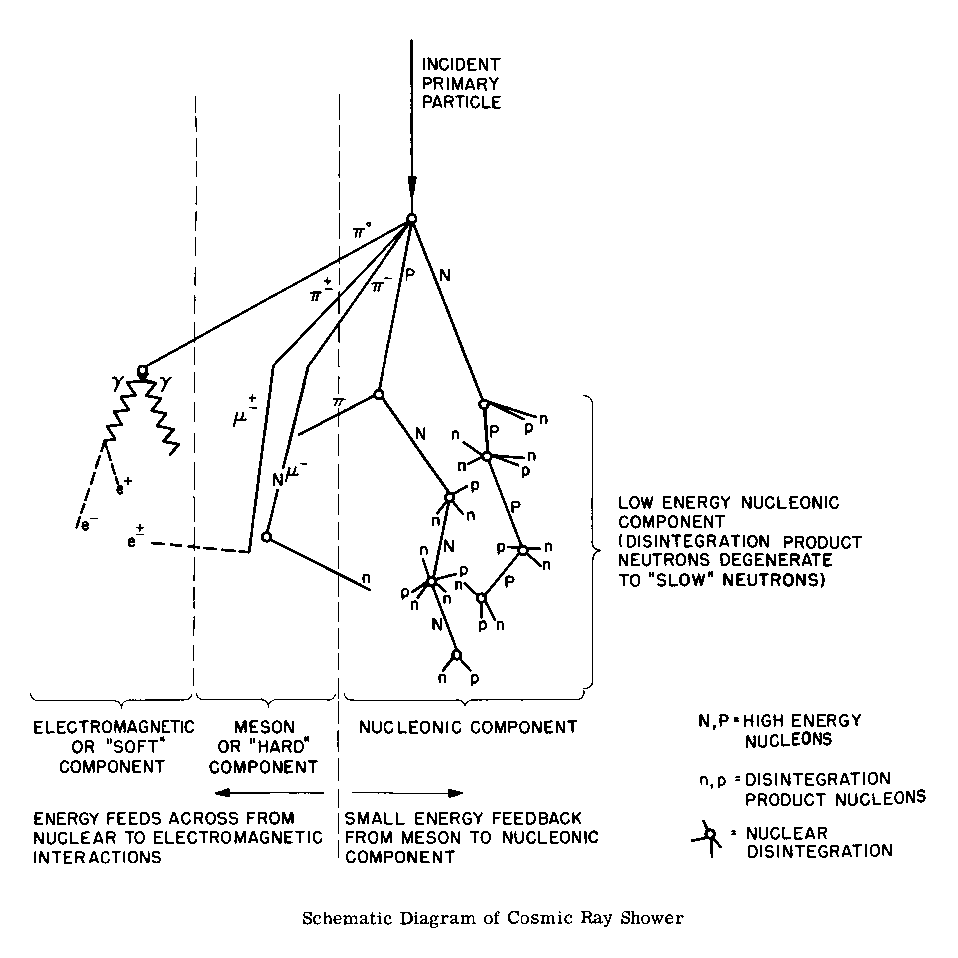
The muons are made in the upper atmosphere as a result of primary cosmic rays interactions which have produced a shower of particles, some of which decay into muons. Due to attenuation in the atmosphere of the other shower components, only muons tend to be left at sea level.
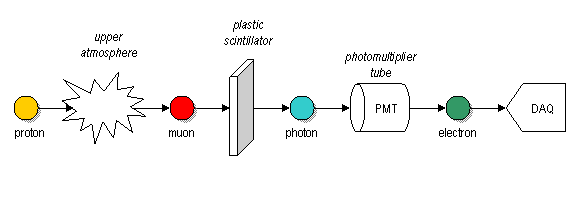
Detection mechanism
Muon flux
Measuring the flux of muons of cosmic ray origin at different heights above the earth is an important time dilation experiment in relativity.
Muon rate at sea level can be estimated as slightly less than one muon per square centimeter, per minute, per steradian.
This can be compared to a solar neutrino flux of about 5E6 per square centimeter per second.
The mean energy of muons reaching sea level is about 4 GeV. Muons, being charged particles, interact with matter by ionizing it. The loss of energy by muons passing throught he atmosphere is proportional to the amout of matter they traverse. The medium is usually characterized by its density (g/cm3) times the distance traveled in centimeters. This is sometimes called the "interaction length" and is measured in g/cm2. The energy loss for muons is about 2 MeV per g/cm2. The interaction depth of the atmosphere is about 1000 cm2, so muons lose about 2 GeV in passing through the atmosphere. With the sea level mean energy of muons detected at the surface = 4 GeV, this suggests an original muon energy in the neighborhood of 6 GeV.
Most muons are thought to be created at altitudes of about 15000 meters and travel with other particles to the Earth in conical showers within about 1° of the trajectory of the primary particle which creates them. Measurement of muon flux at different altitudes is a useful example of relativistic time dilation. With an energy of 4 GeV, the time dilation factor is g = 38.8.
The following empirical formula gives a good approximation to the number at sea level as a function of zenith angle:
Where Iv = 0.0083 cm-2 s-1 sr-1 and φ is the zenith angle (Rossi 1948).
is the number of muons incident on differential area dA during the time dt within the solid angle dω from the direction normal to dA. Integrating this function over the appropriate solid angle, the total flux from all directions can be estimated.
Muon intensity may vary not only with the altitude and angle from vertical but also with latitude and time of night (i.e. the relative position of the sun and the earth s magnetosphere).
Related info:
Relativistic Effects on Muons
The muons have a half-life of 2.2 microseconds. At the speed of light this would give a range of only 660 m. However, at relativistic speeds, the lifetime of the muon, as we perceive it, is much longer. Given a minimal 2 GeV muon (rest mass = 0.1 GeV):
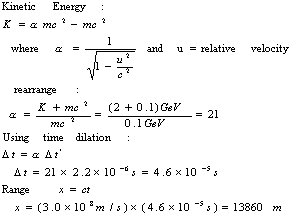
Related info:
Muon lifetime
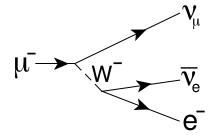
Since the muon is heavier than the electron and is in the same family, the muon will decay into an electron. In order to satisfy conservation laws for leptons, the decay is into an electron and two neutrinos.
Muons lose about 2 MeV of energy per gram per square cm of material that they traverse. Thus muons with less than about 50 MeV will stop in the scintillator (about 0.3%). These stopped muons will decay within several microseconds, emitting an energetic electron which excites atoms in the scintillator producing another pulse of light. The distribution of these times can be related to the muon lifetime.
The free muon decay lifetime is well measured and has been determined to be
However, only the positive muons will decay freely 100% of the time. Negative muons also have another disappearance channel in matter, which is muon capture by a proton resulting in a neutron plus neutrino. This has the possibility of happening to a negative muon, since a negative muon will be captured into a Bohr orbit about the nucleus like an electron, but with a Bohr radius about 200 times smaller than that of the electron. The resulting small radius orbit effectively means that the negative muon spends a large fraction of time inside the nucleus, and thus will have a sizeable probability to be captured by one of the protons inside the nucleus. Since the total decay for negative muons now consists of the sum of the free decay rate plus the capture rate, the lifetime of negative muons in matter will differ from that of positive muons. The capture rate for negative muons will obviously be Z dependent, and it turns out that the free decay rate and the capture rate are about equal for Z=10. Thus for Z=10 the negative muon lifetime would then be 1/2 the positive muon lifetime. It is also the case that the capture rate goes as Z4, so the above information will allow you to calculate the capture rate for any effective Z, given the free muon decay rate. In this experiment you will be measuring the average lifetime of a mix of positive and negative cosmic ray muons stopping in scintillator. Plastics/mineral oil/etc are CH2 chains with an effective Z of about 5.
Charge ratio can be estimated to be µ+/µ- = 1.2 (45% µ- and 55% µ+) and lifetime due to nuclear capture in carbon is aprox 1.93 μs (0.142 μs in iron). And we will measure both: 2.2 μs x 0.55 + 1.9 μs x 0.45 = 2.065 μs.
This is an approximation, but the important thing is that the measured value must be smaller than 2.2 μs value for free decay.
NOTE: Signals produced by stopping muons is much larger than from passing ones.
Related info:
References:
Muon Physics (PDF) by Coan and Ye,
apparatus published as
A Compact Apparatus for Muon Lifetime Measurement and Time Dilation Demonstration in the Undergraduate Laboratory.
Muon mass
If the muon decays at rest (a good approximation for muons that stop in the detector), then the total kinetic energy of the electron and neutrinos will be approximately equal to the rest mass of the muon. The reaction must obey conservation of momentum.
The case of maximum energy electron is when it is ejected in the opposite direction of the two neutrinos (the electron carries half of the kinetic energy). The mass of the muon can be determined measuring the cutoff of the emited electron energy distribution.
The electron pulse heigth distribution must be calibrated in terms of energy. The peak of the muons that pass all the detectors can be used (minimum ionizing muon). See -dE/dx as a function of muon energy (Particle Physiscs Booklet).
This is a difficult task, but measured value should be close to:
Fermi constant
Having mesured τμ and mμ, The Fermi constant GF can be determined.
