Clase 17 - La luz. Fenómenos luminosos. Radiometría y Fotometría.
Prof. Juan Mauricio Matera
7 de junio
La Luz y sus propiedades
¿Cómo se comporta la luz?
Una primera respuesta está relacionado con aquél elemento del ambiente que necesitamos para poder ver.
Es producida por el sol y las estrellas, así como por cuerpos que se encuentran a altas temperaturas, al quemar ciertas substancias.
- También observamos que puede producirse en situaciones que no involucran altas temperaturas, como por ciertos cuerpos que fueron expuestos previamente iluminación (fosforecencia), por ciertos organismos vivos (ej: luciernagas), por descargas eléctricas (relámpagos, arco eléctrico) y por disposutivos electrónicos (luces LED).
La luz como una forma de energía
En todos los casos, la producción de luz involucra el consumo de alguna forma de energía (de origen químico, eléctrico, etc).
Ciertos dispositivos, así como los organismos vegetales, son capaces de obtener energía de la luz.
Cuanto mayor sea la intensidad de la luz, su producción requiere más energía, y es capaz de producir efectos mayores sobre los cuerpos iluminados.
Podemos decir entonces que la luz es una forma de energía que es irradiada por una fuente, se propaga a través del espacio, e interactúa con nuestros ojos para producir una sensación visual, así como con otros sistemas físicos.
Otras propiedades
- Además de la intensidad, la luz tiene otras propiedades:
- Color
- Polarización
- Coherencia
- Velocidad de propagación.
Color
- No percibimos la luz producida por el sol igual que la producida por una vela.
- Por otro lado, cuando la luz atraviesa o se refleja en un medio, esta propiedad cambia.
- Al mezclar luz de diferentes colores, percibimos colores distintos, y más brillantes.
- Al mezclar tintes de colores distintos, el color que reflejan cambia, y se oscurece.
- La luz blanca se descompone en luz de diferentes colores al atravesar ciertos cristales.
Polarización
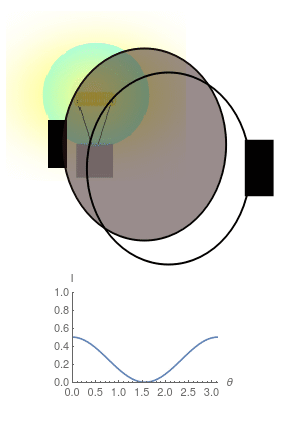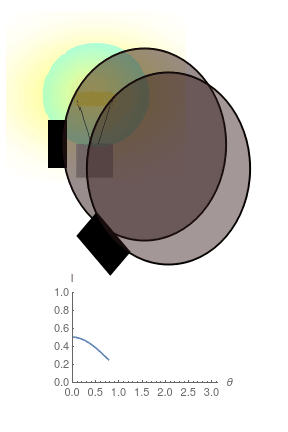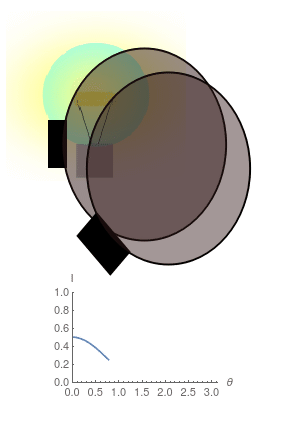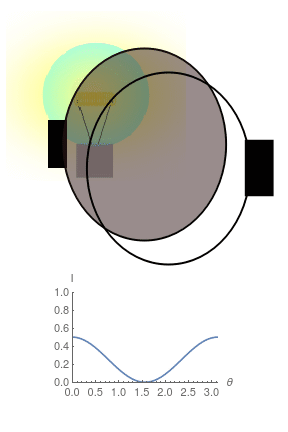
- Existen materiales, llamados polarizadores, que al interponerse entre ciertas fuentes de luz y el ojo, dejan pasar diferente intensidad de luz dependiendo de cómo se orientan.
- Etienne-Louis Malus, descubrió que la ley, que lleva su nombre:
- La intensidad que atraviesa un polarizador es proporcional a* \(a + b\cos(\Theta)^2\).
- Si para una fuente de luz \(b\neq 0\), decimos que la fuente está polarizada.
- Si entre un polarizador y una fuente no polarizada interponemos un segundo polarizador, la luz que atraviesa el segundo polarizador resulta estar polarizada.
- Conclusión: La luz posee una propiedad vectorial a la que llamamos Polarización.
Coherencia
- Se observa en haces monocromáticos.
- Cuando está presente, la intensidad de la luz proyectada sobre una pantalla por dos fuentes no es la suma de las contribuciones individuales: aparecen fenómenos de interferencia.
- Motiva a asumir que la luz se propaga como lo hacen las ondas mecánicas.

Velocidad de propagación
- En 1676 Ole Christensen Rømer estima por primera vez esta velocidad, mediante observaciones astronómicas.
- En el s. XVIII, James Bradley mejora estas medidas y estima que la luz del sol tarda \(8{\rm min}\, 12{\rm s}\) en alcanzar la tierra.
- En 1848, Hyppolyte Fizeau determina la velocidad de la luz en un experimento de laboratorio, obteniendo una velocidad de \(\approx 3 \times 10^{8}{\rm m}/{\rm s}\), de acuerdo con la estimación de Bradley.
- En 1926, Albert Michelson logra una determinación de \(c=2.99796(4) \times 10^{8}{\rm m}/{\rm s}\)
- En la actualidad, el metro fue redefinido de forma que \(c=2.99792458 \times 10^{8}{\rm m}/{\rm s}\) es el valor exacto.
- Al atravesar un medio material, la velocidad de la luz se reduce, originando el fenómeno de refracción.
La Óptica
- Viene del griego clásico optike, que significa “aspecto, apariencia”.
Es la rama de la física que involucra el estudio del comportamiento y las propiedades de la luz, incluidas sus interacciones con la materia, así como la construcción de instrumentos que se sirven de ella o la detectan.
Es una de las ramas más antigüas de la física.
Los primeros desarrollos teóricos sobre la luz datan de la antigua grecia.
Será el tema de las siguientes clases.
Modelos para la luz
- Identificamos a la luz como una forma de energía que irradian ciertos cuerpos.
- Esto no dá aún un “modelo” sobre de qué esta hecha la luz.
- A mediados del sXVII, competían dos modelos:
- Modelo Corpuscular
- Modelo Ondulatorio
- Christian Huygens en 1690, propone una teoría que describe a la luz como un fenómeno ondulatorio.
- En 1704 Isaac Newton publica su Optika donde propone que la luz está compuesta de partículas, y que la luz blanca es el resultado de mezclar luz de diferentes colores.
- Alrededor de 1800, Thomas Young demuestra la existencia del fenómeno de interferencia, lo que dá evidencia experimental a la teoría ondulatoria.
- en 1845, Michel Faraday descubre que los campos magnéticos afectaban la polarización de la luz.
- En 1850, Leon Foucault determina la velocidad de la luz como \(c\approx 298000{\rm km}/{\rm s}\)
- James Maxwell, con su teoría de las ondas electromagnéticas, nota que la velocidad de propagación de estas coincide con la de la luz, y conjetura que son en realidad el mismo fenómeno.
- Poco después, Heinrich Hertz confirma la teoría de las ondas electromagnéticas generando y detectando por primera vez ondas de radio.
- Ya en el siglo XX, Nikola Tesla y Guglielmo Marconi desarrollan paralelamente las primeras comunicaciones basadas en ondas de radio.
- Max Planck y Albert Einstein desarrollan la teoría cuántica de la luz y la explicación del efecto fotoeléctrico: la luz es onda y partícula a la vez.
- En los años 60, se logró construir por primera vez una fuente LASER. La luz LASER es radiación electromagnética coherente, lo que significa que su frecuencia, fase, polarización y dirección de propagación están altamente definidas.
Modelo Corpuscular
- Propuesto por Pierre Gassendi (1660) e Isaac Newton (1704).
- La luz estaba compuesta por partículas microscópicas, rígidas, elásticas y livianas.
- Los emisores de luz emiten estar partículas en todas direcciones.
- En ausencia de materia, las partículas se mueven en línea recta.
- Los cuerpos opacos pueden absorberlas, o hacer que reboten sobre ellos.

Modelo ondulatorio
- Propuesto por Robert Hook (1678) y Christian Huygens (1690).
- La luz es una onda en un medio elástico, y muy tenue que llena el espacio (ether).
- Predice fenómenos semejantes a los observados en las ondas mecánicas (reflexión, refracción e interferencia).
- En diferentes medios, la velocidad de propagación es diferente.
Teoría de las ondas electromagnéticas de Maxwell
- Desarrollada por James C. Maxwell en 1862.
- La luz es una onda electromagnética que resulta de las perturbaciones sobre los campos electromagnéticos.
- Las perturbaciones son producidas por el movimiento de partículas cargadas.
- La teoría predice que la luz se propaga en el vacío con una velocidad característica \(c\approx 2,99{\rm m}/{\rm s}\), que se reduce al atravesar medios materiales.
- La velocidad de propagación en el vacío es independiente del sistema de referencia!
- La luz visible forma sólo una pequeña parte del espectro electromagnético.
- La analizaremos con detalle estos conceptos a lo largo del curso.
Electrodinámica cuántica
- La teoría de Maxwell presentaba problemas en lo que respecta a describir la emisión de radiación electromagnética por los sistemas atómicos, así como en la descripción del espectro de emisión de los cuerpos calientes.
- La introducción de la mecánica cuántica a principios del s XX resuelve estos problemas al considerar que la luz está compuesta de partículas, ni es una onda.
- En esta teoría, la luz está formada por fotones, objetos que se comportan como ondas o partículas en diferentes situaciones:
- Al ser emitidos o absorbidos por los átomos, lo hacen como partículas puntuales, con una cantidad fija de energía.
- Al propagarse, los fotones lo hacen como ondas, con una frecuencia proporcional a la energía \(E_{\nu}=\hbar f\).
Ondas en 3 Dimensiones
- Soluciones de la Ecuación de onda vectorial tridimensional: \[
c^2\frac{\partial^2 \vec{A}}{\partial t^2} = \frac{\partial^2 \vec{A}}{\partial x^2} + \frac{\partial^2 \vec{A}}{\partial y^2}+\frac{\partial^2 \vec{A}}{\partial z^2}
\] donde
- \(\vec{A}(t,\vec{x})\) es un campo vectorial.
- \(c=2.99\times 10^8{\rm m}/{\rm s}\) es la velocidad de propagación de las ondas.
- Es análoga a la ecuación para las óndas mecánicas en un medio elástico.
- Las ondas electromagnéticas son transversales: \(\vec{A}\) oscila en el plano perpendicular a la dirección de propagación.
- Las soluciones de esta ecuación pueden escribirse como la superposición de ondas planas.
Ondas Planas
- Soluciones básicas de la Ec. de Onda \[
\vec{A}(t,\vec{x})=\vec{A}_0 \cos(\omega t - \vec{k}\cdot \vec{x}+\phi)
\] con
- \(\vec{A}_0=|\vec{A}_0|\check{A}_0\), donde \(|\vec{A}_0|\) dá la Amplitud y \(\check{A}_0\) la dirección de polarización
- \(\phi\) la fase,
- \(\omega\) la frecuencia angular,
- \(\vec{k}\) el vector de onda y
- \(\frac{\omega}{|\vec{k}|}=c\).
- Las superficies \(\omega t - \vec{k}\cdot \vec{x}+\phi=0\) son planos llamados frentes de onda que se desplazan en la dirección de \(\vec{k}\) con velocidad \(c\).
- Las ondas electromagnéticas son ondas transversales: \(\vec{k}\cdot \vec{A}_0=0\).
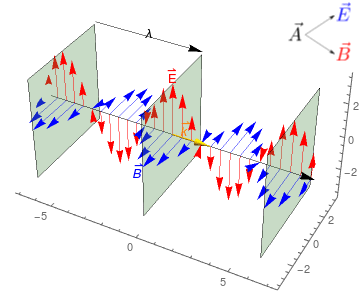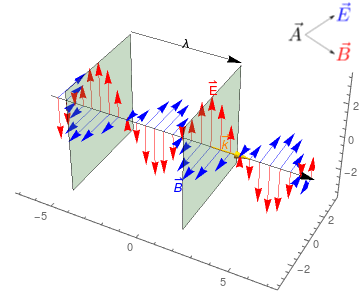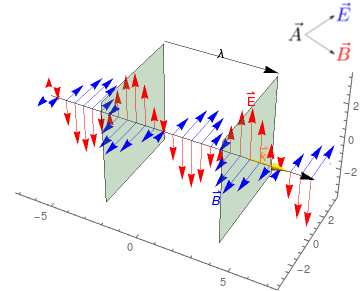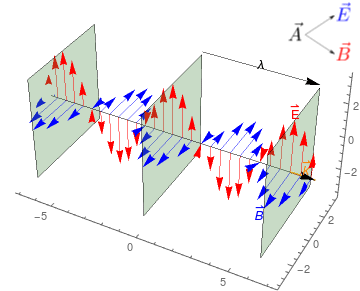
- \(f=\frac{\omega}{2\pi}\) es la frecuencia de la onda.
- \(\lambda=\frac{2\pi}{|\vec{k}|}\) es la longitud de onda de la onda.
Distribución espectral de energía
- En general, una onda electromagnética es una superposición de diferentes ondas planas.
- En la práctica, cada componente de onda plana se comporta de forma independiente.
- Como en las ondas mecánicas, cada componente de onda plana tiene asociada una energía.
- Definimos la Distribución espectral \(P(\lambda)\) (o espectro), de manera que \(P(\lambda)d\lambda\) es la potencia asociada a las componentes en un intervalo \(d\lambda\) de longitudes de onda en torno a \(\lambda\).
- \(P(\lambda)\) es una característica de la fuente de luz.
- \(P(\lambda) \propto A(\lambda)^2/\lambda^2\) con \(A(\lambda)\) la amplitud.
- \(P(\lambda)\) está relacionada con el color con que percibimos la luz.
- Si \(P(\lambda)\) se concentra en un intervalo de ancho \(\Delta \lambda\) en torno a un \(\lambda_0\), con \(\Delta \lambda\ll \lambda_0\), decimos que la onda es aproximadamente monocromática.
- Si \(P(\lambda)\) es aproximadamente uniforme en todo el espectro visible decimos que la luz es blanca.
- Los cuerpos calientes irradian luz según la Ley de Planck, que depende de su temperatura. Sólo una pequeña parte de la energía se produce en el visible.
- Los espectros atómicos poseen múltiples picos, independientes de la temperatura.
- Las fuentes LED’s y Lasers aprovechan esto para producir espectros monocromáticos.
Luz y Radiación.
Radiación
- La luz es una forma de radiación, esto es, de emisión de energía.
- La potencia irradiada por una fuente de luz es la cantidad de energía que irradia por unidad de tiempo.
- Si la fuente es isótropa, la energía irradiada se distribuirá uniformente en todas las direcciones.
- El efecto de esta radiación sobre el ojo, o el sistema físico con el que interactúe estará relacionado con la porción de la potencia radiada que incida sobre este.
- Esta porción dependerá del tamaño del sistema, así como de la distancia a la fuente.
- Llamamos Irradiancia \(E_{\rm Rad}\) en un punto a la potencia recibida, por unidad de área, por un cuerpo situado en ese punto.
En el sistema MKS, la Irradiancia tiene unidades de \[[E_{\rm Rad}]=[{\rm Watt}]/[{\rm m}]^2\]
Irradiancia y Densidad de Flujo
En la definición de irradiancia, debemos ser precisos respecto a qué área es la considerada.
- Consideramos superficies diferenciales planas \(d\vec{S}\).
- Definimos la Irradiancia como el flujo máximo de energía, por unidad de área, respecto a todas las orientaciones de \(d\vec{S}\): \[ E_{\rm Rad}=\left.\frac{dP}{dS}\right|_{d\vec{S}_{max}}= \vec{s}_E \cdot d\vec{S}_{max} \]
- donde introducimos la magnitud vectorial Densidad de flujo \(\vec{s}_E\) como el vector de magnitud igual a la irradiancia, y orientado en la dirección de \(d\vec{S}_{max}\)
- Para una fuente isótropa, \(\vec{s}_E\) apunta en la dirección radial y en sentido saliente desde la fuente.
- Integrando sobre cualquier superficie cerrada \({\cal S}\) que envuelve sólo a la fuente, \[ P_{total}=\oint_{\cal S} \vec{s}_E\cdot d\vec{S} \] es la Potencia total radiada por la fuente.
- En particular, si la fuente es isótropa, podemos deducir de esto que
- \(\vec{s}_E\) debe apuntar en la dirección radial desde la fuente.
- Su magnitud sólo puede depender de la distancia. Luego, \[
\vec{s}_E = \frac{P_{total}\check{r}}{4\pi r^2}\Rightarrow I(r)= \frac{P_{total}}{4\pi r^2}
\] de manera que la intensidad es inversamente proporcional al cuadrado de la distancia a la fuente.
Densidad de flujo y rayos
- La densidad de flujo de energía es un ejemplo de campo vectorial.
- Una representación gráfica más amigable se obtiene en términos de la noción de líneas de flujo.
- Se definen de manera que en todo punto, son tangentes al vector densidad de flujo.
- Podemos pensar a las líneas de flujo como las trayectorias de partículas que transportan la energía asociada a la radiación.
- En la descripción ondulatoria, son curvas normales a los frentes de onda.
- En el contexto de la óptica, nos referimos a estas como rayos. Volveremos a esto la clase que viene.


Intensidad Radiante
- En ciertos casos, es conveniente referirse a la potencia entregada en una dirección de forma independiente a la distancia.
Se introduce entonces la noción de ángulo sólido \(\Omega\), como la el área de la proyección de una superficie sobre una esfera unitaria
- La unidad de ángulo sólido es el estereorradián (\([{\rm sr}]\)): \(0<\Omega< 4\pi\) \[ d\Omega = \frac{dA}{r^2} \]
Definimos entonces la Intensidad Radiante (\(I\)) como la potencia irradiada por ángulo sólido.
Radiancia
- Cuando consideramos fuentes no puntuales, definimos la Radiancia como la intensidad radiante por unidad de área, en cierta dirección.
Luz e Iluminación
- Hasta ahora, analizamos las propiedades físicas de la luz, independientemente de cómo la observamos.
- La descripción cuantitativa de estas propiedades se conoce como Radiometría.
- Vamos a discutir ahora las propiedades de la luz desde el punto de vista de su utilidad para Iluminar, esto es, para ayudarnos a ver.
- La descripción cuantitativa de la capacidad para Iluminar de una fuente de luz se conoce como Fotometría.
- Para avanzar con la descripción fotométrica, necesitamos tener en cuenta las características del ojo como sensor.
El ojo humano
- La Fotometría estudia la luz desde el punto de vista de la sensación visual.
- Involucra únicamante a la región del espectro visible \[ 380{\rm nm} \;\mbox{(UV)} \leq \lambda_{\rm visible} \leq 700{\rm nm} \;\mbox{(IR)} \]
- Es capaz de detectar
- Dirección de origen de la luz
- Intensidad
- Color
- Es insensible a
- Polarización.
- Coherencia.
Formación de imágenes
- Las ondas electromagnéticas inciden sobre el iris con diferentes direcciones de propagación.
- Del iris surge una onda esférica cuyo frente codifica la imagen en un patrón de intensidades.
- Al incidir sobre la pantalla (retina), se forma una imagen invertida.
- La retina convierte el patrón de intensidades en impulsos eléctricos.
- El cerebro interpreta esos impulsos.
Percepción de la intensidad luminosa
- El ojo humano no responde uniformemente a la misma Irradiancia para diferentes longitudes de onda.
Iluminancia, Luminancia, Flujo luminoso e Intensidad Luminosa.
- Para cuantificar la capacidad de la radiación electromagnética para Iluminar debemos ponderar la el flujo de energía con la respuesta del ojo:
- \(E_{Lum}\) es la Iluminancia o densidad de flujo luminoso.
- En el sistema MKS, se mide en Lux \([{\rm Lx}]=[{\rm Lm}]/{\rm m}^2\)
Aquí, Lumen \([{\rm Lm}]\) es la Unidad de flujo luminoso (\(\Phi_{\rm lum}\)) del sistema MKS, y se define como
“El Flujo Luminoso de una fuente monocromática que irradia \(\frac{4\Pi}{683}{\rm W}\) en una longitud de onda de \(555{\rm nm}\)”
Escalas de Irradiancia e Iluminancia
| Fuente | \(E_{\rm rad}\) \([{\rm W}/{\rm m}^2]\) | \(E_{\rm lum}\) \([{\rm Lx}]\) |
|---|---|---|
| Sol + Cielo | \(245\) | \(100\times 10^{3}\) |
| Sol + Cielo nublado | \(200\) | \(10\times 10^{3}\) |
| Interior cerca de ventana | \(25\) | \(1\times 10^{3}\) |
| Luna llena | \(2\) | \(0,2\) |
| Estrella (Sirius A) | \(1\times 10^{-7}\) | \(0,3\times 10^{-3}\) |
| Vela (a \(1{\rm m}\)) | \(1\times 10^{-3}\) | \(1\) |
| LED | \(10\times 10^{-3}\) | \(3\) |
| Lampara incendescente | \(40\) | 40 |
| Lampara Fluorescente | \(40\) | \(200\) |
Intensidad Luminosa
Así como definimos la Intensidad Radiante como el flujo de radiación por unidad de ángulo sólido, definimos la Intensidad luminosa (en una dirección) como el flujo luminoso por unidad de ángulo sólido.
En el sistema MKS se define la Candela \([{\rm cd}]\) como la intensidad luminosa correspondiente a \(1{\rm Lm}\) por \([{\rm sr}]\).
En ausencia de absorción, la intensidad luminosa es independiente de la distancia a la fuente.
Medida cuantitativa de la Iluminancia.
- La Irradiancia cae con el cuadrado de la distancia a la fuente para todas las \(\lambda\) \[ \frac{E_{\rm Lum}^{(1)}}{E_{\rm Lum}^{(2)}}= \frac{E_{\rm Rad}^{(1)}}{E_{\rm Rad}^{(2)}}=\frac{r_2^2}{r_1^2} \]
- Podemos comparar Intensidades luminosas de dos fuentes comparando las distancias a las que producen la misma Irradiancia sobre un cuerpo.
- El fotómetro de Bunsen se basa en este principio.
- En las aplicaciones, se utilizan células fotoeléctricas y otros sensores electrónicos calibrados según la respuesta del ojo.
- En la actualidad, podemos usar un smartphone como luxómetro: Physics Toolbox.
Luminancia
- Cuando consideramos fuentes no puntuales, definimos la Luminancia \(L\) como la intensidad luminosa por unidad de área, en cierta dirección.
- En el sistema MKS, se mide en \([{\rm cd}]/[{\rm m}]^2=[{\rm Lx}]/[{\rm sr}]\).
- Para una superficie reflejante, \[ L=\frac{1}{\cos(\theta)} \frac{dI^{\rm sup}_{\rm lum}}{dA}= \frac{\alpha}{\cos(\theta)} \frac{dI^{\rm fuente}_{\rm lum}}{dA} \]
Relación entre Magnitudes Fotométricas
Relación entre Magnitudes Radiométricas y Fotométricas.
Percepción del color
- Diferentes fuentes de luz producen en el ojo diferentes sensaciones a las que llamamos color.
- Como en las ondas de sonido, una onda electromagnética es una superposición de ondas armónicas con diferentes longitudes de onda.
- Llamamos distribución espectral \(P(\lambda)\) a la función que describe la forma en que la energía de la onda electromagnética se distribuye en las diferentes longitudes de onda \(\lambda\).
- La percepción del color está relacionada con cómo percibe el ojo la distribución espectral de la luz.
Cromaticidad
- El ojo humano, como la antena de una radio, es capaz de sintonizar esas longitudes de onda, en el intervalo \(\approx 380 - 780 {\rm nm}\).
- Si la distribución espectral es aproximadamente uniforme en ese intervalo, decimos que la fuente produce luz blanca.
- El ojo no es capaz de distinguir la luz monocromática de la mezcla de luces de diferentes colores.
- La cromaticidad es la medida cuantitativa de la sensación de color. Tiene dos aspectos
- Matiz: Relacionado con la posición del máximo de \(P(\lambda)\)
- Saturación Relacionado con el ancho de \(P(\lambda)\).
El color de los objetos
- Al interactuar con la luz, las superficies de los cuerpos absorben de manera diferente la radiación a diferentes longitudes de onda, reflejando el resto.
- El cerebro asigna color a una superficie en función del color de la luz que refleja.
- Bajo diferentes condiciones de iluminación, la misma superficie puede aparentar diferentes colores.
- Los pigmentos son substancias que absorben luz en longitudes de onda específicas.
- Mediante pigmentos es posible colorear la luz que refleja una superficie o que transmite un cuerpo.
- Mezclando Pigmentos es posible lograr diferentes colores bajo luz blanca.
Generación y mezclas de colores
- Los colores primarios o básicos son aquellos cuya combinación produce todos los demás.
- En imprentas son el cyan, el magenta y el amarillo.
- En iluminación son el azul (B - blue), el verde (G - green) y el rojo (R - red).
- Cualquier otro color se puede obtener combinándolos en diferentes proporciones. Así los secundarios se obtienen con mezclas al 50%; los terciarios mezclando dos secundarios entre sí, etc.
Las mezclas, que en luminotecnia se consiguen mediante filtros y haces de luces, pueden ser aditivas o sustractivas.
- Mezclas aditivas u ópticas: se obtienen sumando haces de luces de colores. Si la suma da blanco, los colores son complementarios.
- Mezclas sustractivas o pigmentarias se consiguen aplicando filtros sucesivos a la luz blanca.
Fuentes de luz
- Una Fuente de luz es un dispositivo que convierte energía en flujo luminoso.
- Para producir Flujo Luminoso una fuente debe consumir energía.
- Esta energía se distribuye en
- Energía Radiante
- En el visible (útil)
- Fuera del visible (radiación IR y UV)
- Energía disipada por otros mecanismos.
- Energía Radiante
- La relación entre el flujo luminoso que produce una fuente y la potencia invertida en producirlo es el Rendimiento o Eficacia de la fuente. \[ R= \frac{\Phi_{\rm lum}}{P_{\rm consumida}} \]
- En el sistema MKS, se mide en \([{\rm Lm}]/[{\rm W}]\).
- La Eficacia Relativa \(k\) representa el porcentaje de la energía radiada en el visible, y se expresa como \[ k = \frac{\int V(\lambda) P(\lambda)d\lambda}{ \int P(\lambda)d\lambda} \times 100\% \]
Mecanismos Físicos de producción de luz
- Radiación térmica (cuerpo negro).
- Radiación en equilibrio térmico con la fuente.
- Distribución de cuerpo negro \(P(\lambda)\approx \frac{2\pi c^2 h \lambda^{-5}}{\exp\left(\frac{h c}{k T \lambda}\right) -1}\).
- Emisión química (liberación de energía de ligadura).
- Emisión en longitudes de onda características.
- Típicamente en el espectro infrarrojo- visible.
- Desexcitación atómica (fluorescencia, fosforescencia)
- Líneas espectrales definidas.
- Rango visible - UV.
Luz solar
- Se produce por reacciones nucleares en el interior del sol.
- Es gratis.
- Distribución espectral \(\approx\) de cuerpo negro a \(5600^o C\) (pico en \(480{\rm nm}\))
- Irradia una potencia total de \(3,828\times 10^{26}{\rm W}\)
- Equivale a una intensidad luminosa de \(24\times 10^{26}{\rm cd}\).
- A la tierra llegan \(10^5 {\rm Lx}\).
- Vida útil: \(10000 M\) años.
Llama
- Se produce por la combustión de un hidrocarburo (aceite, parafina, petroleo, etc)…
- La más antigua forma de iluminación artificial.
- Dos contribuciones: térmica (cuerpo negro \(\approx 1500-4000^o{\rm C}\)) y emisión atómica característica.
- Intensidad radiante \(1 - 10 {\rm cd}\).
- Eficacia luminosa de entre \(0,3\) y \(2{\rm Lm}/{\rm W}\).
- Sólo entre el \(0,04\%\) y el \(0,3\%\) es irradiado en el visible.
Lámparas Incandescentes
- Se produce como radiación térmica (cuerpo negro) vía efecto Joule.
- Distribución de cuerpo negro alrededor de \(2500^o{\rm C}\) (luz cálida, \(\lambda_{\rm max}\approx 1000{\rm nn}\)).
- Irradia el \(75\%\) de la potencia eléctrica consumida, pero sólo el \(15\%\) en el rango visible.
- Eficacia: 10-20 \(lm/W\).
- La eficacia mejora en el caso de las lámparas halógenas, que pueden trabajar a mayor temperatura.
- Vida Útil: \(1000\) horas.
Lámparas Fluorescente
- Se produce en dos etapas:
- ionización de un gas (produce radiación UV)
- fluorescencia (una película de material absorbe UV y reemite en visible).
- Distribución discontinua.
- Efecto estroboscópico (\(50{\rm Hz}\))
- Irradia el \(75\%\) de la potencia eléctrica consumida, pero sólo el \(15\%\) en el rango visible.
- Flujo luminoso \(\approx 400-8000{\rm Lm}\).
- Rendimiento: 50-80 \(lm/W\).
- Vida Útil: \(1000\) horas.
- Residuo peligroso (\(Hg\)).
Lámpara LED
- Se produce por desexcitación electrónica en un semiconductor.
- Distribución centrada en una \(\lambda\) específica.
- Color e intensidad controlables electrónicamente.
- Intensidad de \(1-1000{\rm lm}\)
- Hasta \(200{\rm lm}/{\rm W}\). Limitada por el circuito de alimentación.
- Vida útil \(22000\) horas.