Clase 11 - Ley de Faraday. Aplicaciones.
Prof. Juan Mauricio Matera
12 de abril de 2019
Repaso y motivación.
- El campo electrostático \(\vec{E}\) es generado por las cargas eléctricas.
- Este satisface las ecuaciones
- La Ley de Gauss: \(\int\int_{\cal S}\vec{E}\cdot d\vec{\cal S}=\frac{Q_{\cal S}}{\varepsilon_0}\) para cualquier superficie cerrada \({\cal S}\)
- La Ley de campo conservativo: \(\int_{\cal C}\vec{E}\cdot d\vec{\ell}=0\) para cualquier curva \({\cal C}\).
- El campo magnético \(\vec{B}\) es originado por corrientes eléctricas.
- El campo magnético en sistemas estacionarios satisface
- La Ley de Gauss: \(\int\int_{\cal S}\vec{B}\cdot d\vec{\cal S}=0\) para cualquier superficie cerrada \({\cal S}\)
- La Ley de Ampère: \(\int_{\cal C}\vec{B}\cdot d\vec{\ell}=\int_{\cal S}\mu_0 \vec{j}\cdot d\vec{\cal S}=\mu_0 i_{\cal C}\) para cualquier curva \({\cal C}\), cualquier superficie \({\cal S}\) limitada por \({\cal C}\), donde \(i_{\cal C}\) es la corriente neta rodeada por \({\cal C}\).
Vectores Polares vs Vectores Axiales
| Vectores Polares | Vectores Axiales |
|---|---|
| \(\vec{r}\) | \(d\vec{\cal S}= \frac{\partial \vec{r}}{\partial u}\times \frac{\partial \vec{r}}{\partial u} dudv\) |
| \(\vec{v}=\frac{d\vec{r}}{dt}\) | \(\vec{\omega}=\frac{\vec{r}\times\vec{v}}{r^2}\) |
| \(\vec{F}=m \frac{d\vec{v}}{dt}\) | \(\vec{\cal T}=\vec{r}\times \vec{F}\) |
| \(\vec{E}\) | \(\vec{B}=\frac{\mu_0}{4\pi}\oint \frac{d\vec{\ell}\times\check{r}}{r^2}\) |
| \(\vec{p}\) | \(\vec{M}= i \vec{\cal S}\) |
En presencia de campos eléctricos y magnéticos,
- Una partícula de carga \(q\) con velocidad \(\vec{v}\) sufre una fuerza \(\vec{F} = q (\vec{E}+\vec{v}\times \vec{B})\)
- un elemento de corriente estacionaria \(i d\vec{\ell}\) sufre una fuerza magnética \(d\vec{F}=i d\vec{\ell}\times \vec{B}\).
- Un momento magnético \(\vec{M}\) sufre un torque \(\vec{\tau}=\vec{M}\times \vec{B}\) y una fuerza \(\vec{F}= \nabla(\vec{M}\cdot\vec{B})\) que tiende a alinear \(\vec{M}\) con \(\vec{B}\) y arrastrarlo hacia las zonas con mayor intensidad de campo.
- Con estas herramientas analizamos el motor eléctrico.
- Al circular corriente por un solenoide, en presencia de un campo magnético estático uniforme, este sufre un torque \[\vec{\tau}=N (i\vec{\cal S})\times \vec{B}\] donde \(\vec{\cal S}\) es la superficie de una espira, orientada según la circulación de \(i\), \(N\) es el número de espiras, y \(\vec{B}\) es el campo externo.
- Si la espira es forzada a girar en un eje perpendicular a \(\vec{B}\) con velocidad angular \(\vec{\omega}\), la potencia mecánica sobre el motor es
\[P_{\rm mec}=\vec{\omega} \cdot \vec{\tau}=N i \vec{\omega}\cdot \vec{\cal S}\times \vec{B}= i N \|{\vec S}\|\|\vec{B}\|\omega\|\sin(\omega t)\| =N i \left\|\frac{\partial \vec{\cal S}\cdot \vec{B}}{\partial t}\right\|\]
- Desde un punto de vista eléctrico, la potencia eléctrica consumida \(P_{e}\) por un elemento de un circuito eléctrico (como un motor) tiene la expresión \[P_e=\Delta V i\] donde \(\Delta V\) es la caída de potencial en el sentido de circulación de la corriente.
El Motor Eléctrico y el Generador Eléctrico
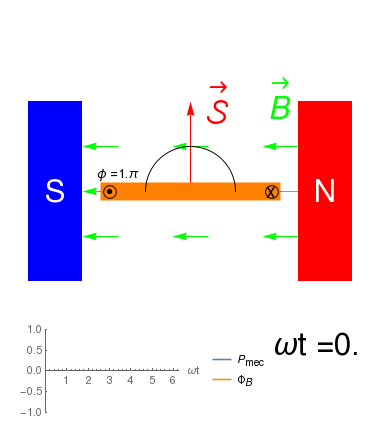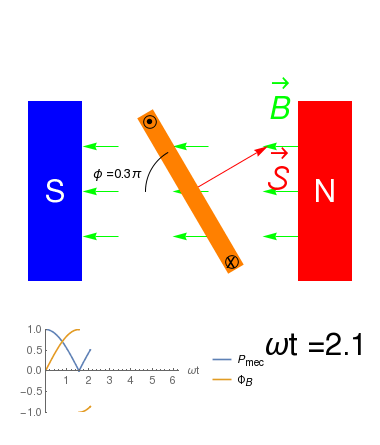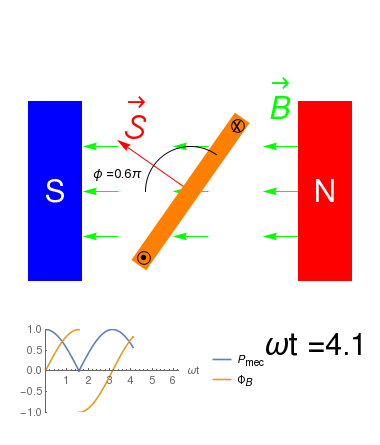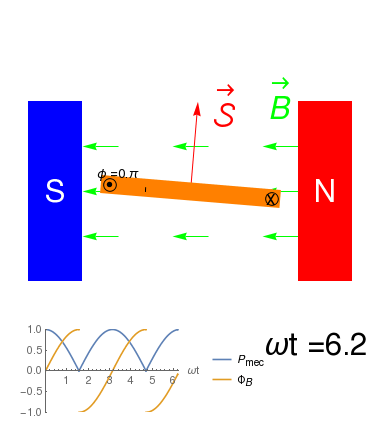
Debido al principio de conservación de la energía, en un motor \[ P_e = P_{dis} + P_{mec}\] donde \(P_{dis}\) es la potencia disipada vía efecto Joule, y \(P_{mec}\) es el trabajo mecánico por unidad de tiempo que realiza el elemento sobre su entorno.
- En el caso del motor, \(P_{dis}= i^2 R=\) donde \(R\) es la resistencia eléctrica del solenoide, y
\(P_{mec}=i \frac{d\Phi_B}{dt}\) donde \(\Phi_B=N\vec{\cal S}\cdot \vec{B}=\|\vec{\cal S}\|\|\vec{B}\|\cos(\omega t)\) es el Flujo Magnético que atraviesa cada espira del solenoide. De esta manera \[ P_{e} = i (\Delta V_R - {\cal E}_{ind})\] con \({\cal E}_{ind}=-\frac{\partial \Phi_B}{\partial t}\) la Fuerza Electromotriz inducida en el solenoide.
Generador Eléctrico
- Es el mecanismo básico detrás de toda la generación de energía eléctrica, desde las dínamos de bicicleta hasta las centrales termoeléctricas.
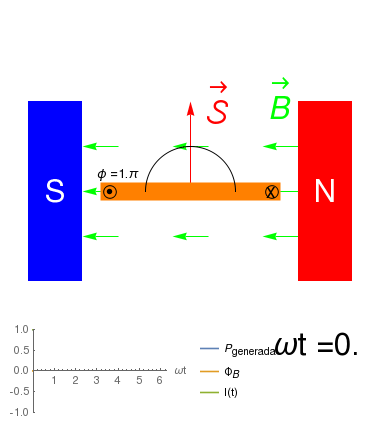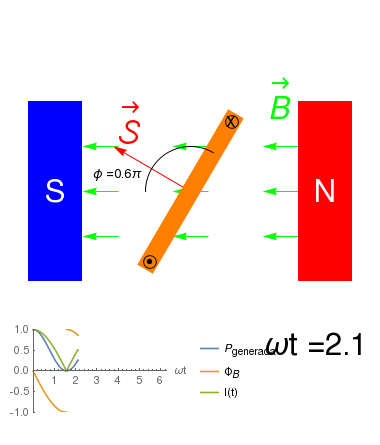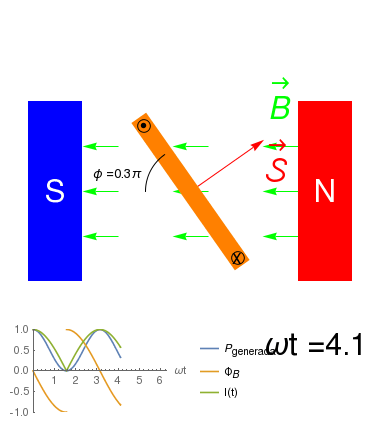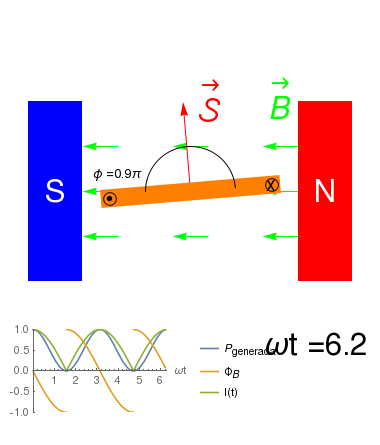
\(\mbox{Fuerza de Lorentz}\Rightarrow{\cal E}_{ind}=-\frac{\partial \Phi_B}{\partial t}\)
- Si el solenoide es forzado a girar en sentido opuesto, \({\cal E}_{ind}\>0\) y por lo tanto el motor genera energía eléctrica.
- Decimos entonces que tal dispositivo es un Generador de energía Eléctrica.
- La corriente que circula en un generador no está fija desde afuera: es forzada a moverse por la Fuerza de Lorentz.
- Debido a que la \({\cal E}_{ind}\) no es constante, \(i\) tampoco lo es.
- El sentido de \(i\) dependerá del sentido de giro del generador.
Alternadores
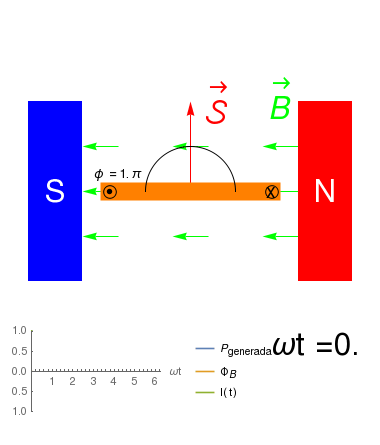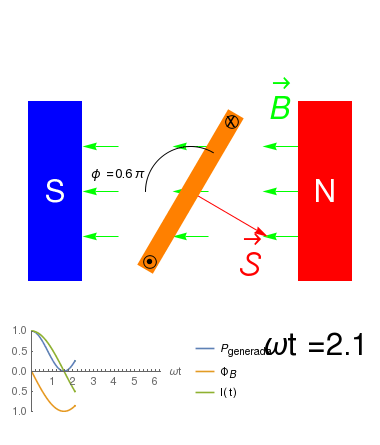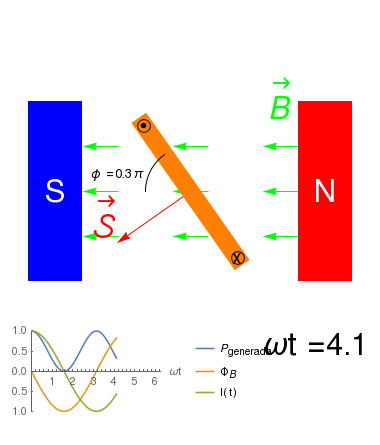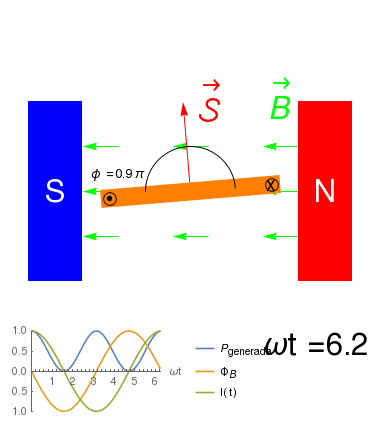
\({\cal E}_{ind}=-\frac{\partial \Phi_B}{\partial t}\)
- Cambiando la forma de los contactos, de manera que la corriente siempre circule en el mismo sentido, el generador producirá una FEM \[\begin{eqnarray*} {\cal E}_{ind} &=& -\frac{\partial \Phi_B}{\partial t}\\ &=& -N B \frac{\cos(\omega t)}{\partial t}\\ &=&-N \omega B \sin(\omega t) \end{eqnarray*}\]
Decimos entonces que el sistema produce una FEM alterna, y se lo llama Alternador.
Alternador invertido: Solenoide fijo e iman rotante
- Es posible construir un alternador en el que son los imanes los que se mueven, en lugar del solenoide, comprobandose que también \[{\cal E}_{ind}=-\frac{\partial \Phi_B}{\partial t}\] donde la variación de \(\Phi_B\) es debida al cambio en \(\vec{B}\,.\)
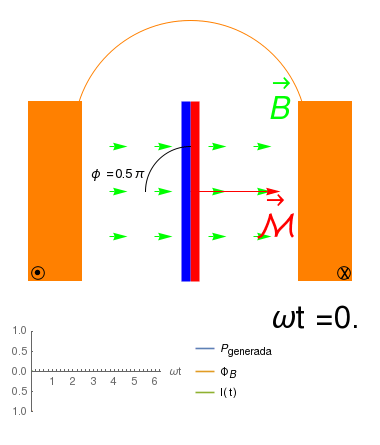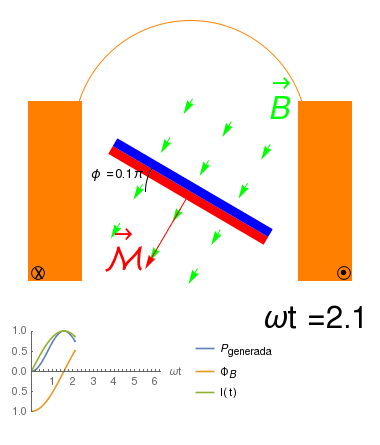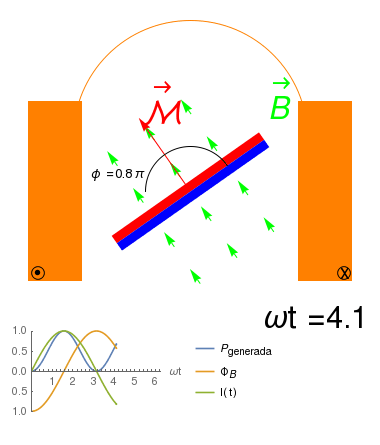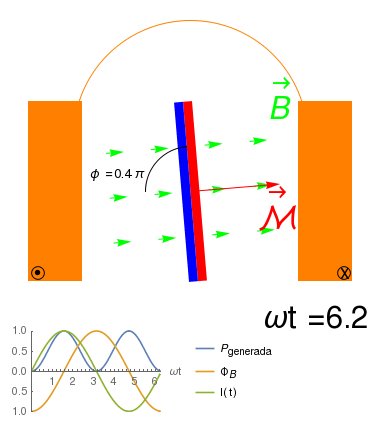
- Observamos que en este caso, \({\cal E}_{ind}\) existe aún sin un transporte neto de carga en el solenoide, por lo que no podemos explicarla en términos de la Fuerza de Lorentz sobre los portadores: estos se mueven como si estuvieran en presencia de un campo eléctrico externo \(\vec{E}\). En tal caso, \[{\cal E}_{ind}=\oint \vec{E}\cdot d\vec{\ell}\]
- \({\cal E}_{ind}\) no depende ni de los portadores de carga ni del conductor: \(\vec{E}\) sólo se diferencia del campo electrostático en que \(\oint \vec{E} \cdot d\vec{\ell}\neq 0\)
Ley de Fadaray
Michel Faraday
- Fue el primero en unificar la descripción de los fenómenos eléctrostáticos.
- En 1821 creo el primer motor eléctrico
- en 1834 publicó las leyes de la electroquímica.
- Introdujo las nociones de líneas de campo, y acción a distancia.
Ley de Faraday
- En 1932, Faraday realizó una serie de experimentos, cuyos resultados se reducen en la Ley de Inducción que lleva su nombre: \[ {\cal E}_{ind}=\oint_{\cal C} (\vec{E}+\vec{v}_{\cal C}\times\vec{B})\cdot d\vec{\ell}=-\frac{\partial }{\partial t}\int\!\!\!\int_{\cal S} \vec{B}\cdot d\vec{\cal S} \] donde \({\cal C}\) es un camino conductor, \(\vec{v}_{\cal C}\) es la velocidad con que se desplaza \({\cal C}\), y \({\cal S}\) cualquier superficie limitada por este.
\[ {\cal E}_{ind}=\oint_{\cal C} (\vec{E}+\vec{v}_{\cal C}\times\vec{B})\cdot d\vec{\ell}=-\frac{\partial }{\partial t}\int\!\!\!\int_{\cal S} \vec{B}\cdot d\vec{\cal S} \]
- Si \({\cal C}\) se mueve, pero \(\vec{B}\) es constante, recuperamos la Ley de Fuerza de Lorentz.
- Si \({\cal S}\) (y por lo tanto \({\cal C}\) es constante, pero \(\vec{B}\) varía en el tiempo, las cargas se mueven como en presencia de un campo eléctrico No Conservativo.
- Si \({\cal C}\) no coincide con un camino conductor, la segunda igualdad sigue siendo válida, pero no podemos hablar de Fuerza Electromotriz inducida.
- Si \({\cal S}\) es constante, la expresión se reduce a la Ley de Maxwell-Faraday \[ \oint_{\cal C} \vec{E}\cdot d\vec{\ell}=-\int\!\!\!\int_{\cal S} \frac{\partial \vec{B}}{\partial t}\cdot d\vec{\cal S} \]
- Vía el teorema de Stokes, esta ley puede expresarse en forma equivalente como \[ \nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\]
Ley de Lenz
El signo negativo frente a la derivada temporal puede deducirse de la consistencia de la teoría con la conservación de la energía: En presencia de un conductor, una variación de \(\vec{B}\) induciría una \({\cal E}_{ind}\) que originaría una corriente, que a su vez produciría un campo \(\vec{B}'\), que incrementaría aún más la variación del flujo magnético, y el proceso nunca se detendría.
- Henrich Lenz llegó a esta conclusión y la enunció de esta manera: “Una variación de \(\Phi_B\) inducirá una \({\cal E}_{ind}\) de manera que el campo magnético asociado a la corriente se opondrá a la variación de flujo magnético que le dió origen”.
Corrientes de Foucault
- En la zona cubierta por el imán, debido al campo magnético y a la velocidad del conductor, se establece una separación de carga.
- En los bordes laterales, donde el campo magnético cambia, se establecen corrientes, según la Ley de Lenz.
- El campo se acopla sólo a las corrientes inmersas en él, resultando en una fuerza neta de arrastre.
- La presencia de huecos no modifica el resultado.
- En el caso del péndulo con forma de peine, debido a que la Ley de Faraday sólo aplica a caminos conductores, sólo predice la acción de una fuerza cuando el borde del imán pasa por uno de los dientes, por lo que el efecto es mucho menor.
Freno Magnético
Autoinductancia e Inductancia Mutua
Autoinducción
- Todo circuito cerrado, por el que circula una corriente produce un campo magnético.
- El flujo magnético a través del área que encierra el circuito es proporcional a la corriente que por él circula. \[ \Phi_B= L i \] donde \(L\) es una constante positiva conocida como autoinductancia del circuito. Nótese que \(\Phi_B\) debe ser evaluado en el sentido de la circulación de la corriente.
- Si en el circuito la corriente varía a razón \(\frac{di}{dt}\), la Ley de Inducción de Faraday implica la existencia de una \({\cal E}_{ind}\) o fuerza contra-electromotriz en el circuito tal que \[ {\cal E}_{ind}=-L \frac{di}{dt} \]
- Típicamente, \(L\) para un circuito corto respecto a la sección de los conductores puede despreciarse. Sin embargo, si en el circuito se incluyen solenoides es posible lograr flujos magnéticos relativamente grandes y en forma localizada. En tal caso, se define la autoinducción \(L\) del elemento como aquella que se obtendría al incluir ese elemento en un circuito de autoinducción despreciable.
- Para un solenoide, \(L=\frac{\Phi_B}{i}={\cal S} \mu_0 n N ={\cal S} \mu_0 N^2/\ell\).
Inducción Mutua
Dados dos circuitos \({\cal C}_1\) y \({\cal C}_2\), el campo debido a la corriente que circula por \({\cal C}_1\) induce un flujo en \({\cal C}_2\) tal que \[\Phi_{B}^{(2)}=M_{12} i_1\,.\] Llamamos la Inductancia Mutua \(M_{12}\) a la constante
- Por el principio de acción y reacción, \[\Phi_{B}^{(1)} =M_{21} i_2\] con \(M_{21}=M_{12}\).
- De esta manera, por la Ley de Faraday una variación en la corriente en el circuito \({\cal C}_1\) inducirá una \({\cal E}_{ind}\) en el circuito \({\cal C}_2\) \[{\cal E}_{2}=-M_{12}\frac{di}{dt}\]
En general, la inducción mutua entre conductores es relativamente pequeña, salvo que los circuitos incluyan solenoides acoplados magnéticamente.
Este es el principio básico de los transformadores de corriente alterna.
- Para dos solenoides enrollados sobre un mismo eje, con secciones \({\cal S}_1\) y \({\cal S}_2<{\cal S}_1\), número de espiras \(N_1\) y \(N_2\) y longitudes \(\ell_1\)y \(\ell_2<\ell_1\), \(M_{12}={M}_{21}= \mu_0 N_1 N_2 {\cal S}_2/\ell_2\)
Representación de componentes inductivos en circuitos
Unidades de Inductancia y Autoinductancia
- En el sistema internacional la unidad de Inductancia (y de inductancia mutua) es el Henry o Henrio (\({\rm H}\)). Algunos valores aproximados de \(L\) son
- Cables, \(L\approx 10^{-7}{\rm H}/{\rm m}\)
- Lámpara incandescente, \(L\approx 100{\rm mH}\)
- Lámpara fluorescente \(\approx 1{\rm H}\)
- Motor eléctrico \(\approx 10{\rm H}\)