Repaso de la clase anterior

• Campo eléctrico de una carga puntual en \(\vec{r}_0\) \[ \vec{E}(\vec{r})=\frac{q}{4\pi\varepsilon_0 |\vec{r} -\vec{r}_0|^2}\hat{r}\;\;\;\;\; \hat{r}=\frac{\vec{r} -\vec{r}_0}{|\vec{r} -\vec{r}_0|} \]
• Modelo del dipolo eléctrico
  • Distribución de carga no trivial, con carga neta nula.
  • Caracterizado por \(\vec{p}\) el momento dipolar eléctrico.
  • Para dos cargas de igual magnitud \(|q|\) y signo contrario, separadas por una distancia \(d\), \(\vec{p}=|q|\vec{d}\).
  • Los medios materiales se polarizan en presencia de campos externos, es decir, adquieren momento dipolar.
  • Torque sobre un dipolo \({\cal T}=\vec{p}\times \vec{E}\). Los dipolos se alinean con el campo eléctrico externo.
    
  • Campo eléctrico de un Dipolo Eléctrico \[ \vec{E}(\vec{r})=\frac{3 \frac{(\vec{p}\cdot \vec{r})\vec{r}}{|\vec{r} -\vec{r}_0|^2}-\vec{p}}{4\pi\varepsilon_0 |\vec{r} -\vec{r}_0|^3} \]

• Método de las líneas de campo
  • Consiste en dibujar las líneas integrales del campo eléctrico.
  • Estas líneas presentan las mismas simetrías que el campo eléctrico.
  • En todo punto son tangentes al campo eléctrico.
  • La densidad de líneas en torno a un punto da cuenta de la magnitud del campo.
  • Salen de cargas positivas y terminan en cargas negativas.
  • Dos líneas sólo se cruzan sobre las cargas eléctricas.
  • Permite visualizar el campo eléctrico.
    
  • Método cualitativo para estimar el campo eléctrico en torno a distribuciones de carga.

• Concepto de Flujo de un campo vectorial \[ \Phi = \int_{\cal S} \vec{W}\cdot d\vec{\cal S} \]
• Interpretaciones:
  • Proporcional al número de lineas de campo que atraviesan una superficie.
  • Cantidad de substancia / partículas / energía que atraviesa una superficie por unidad de tiempo.
• Teorema de Gauss: \[ \int_{\cal S} \vec{W}\cdot d\vec{\cal S}=\int_{\Omega} \nabla \cdot \vec{W} d\Omega\] con \({\cal S}\) una superficie cerrada y \(\Omega\) el volumen que esta encierra. \(\nabla \cdot \vec{W} = \frac{\partial W_x}{\partial x}+\frac{\partial W_y}{\partial y}+\frac{\partial W_z}{\partial z}\) es la divergencia del campo \(\vec{W}\).
  • Identidad matemática.
  • Relaciona el flujo de un campo con la integral de su divergencia (asumiendo que esté definida).
  • La divergencia de un campo es independiente de la elección de los ejes de coordenadas (es una magnitud escalar).

• Ley de Gauss “El flujo del campo eléctrico a través de una superficie cerrada es proporcional a la carga que encierra dicha superficie”. \[ \int_{\cal S} \vec{E}\cdot d\vec{\cal S}=\frac{Q}{\varepsilon_0} \] con \(\varepsilon_0=8.85\rm{pF}\rm{m}^{-1}\)
  • Es una ley fundamental de la naturaleza.
  • Expresa un hecho experimental
  • El teorema de Gauss permite expresar esta ley en forma diferencial \[ \nabla \cdot \vec{E}=\frac{\rho}{\varepsilon_0} \]
  • La Ley de Coulomb es una consecuencia de la Ley de Gauss y de la simetría esférica de las cargas puntuales.

• Campos en conductores y Ley de Gauss
  • El campo en el interior de un conductor en equilibrio se anula.
  • El campo sobre la superficie de un conductor en equilibrio es normal a esta.
  • Debido a la Ley de Gauss la carga en un conductor en equilibrio sólo puede alojarse en su superficie.
  • Justo sobre la superficie de un conductor en equilibrio, el campo eléctrico viene dado por \(\vec{E}=\frac{\sigma}{\varepsilon_0}\hat{n}\) donde \(\sigma\) es la densidad superficial de carga en el punto, y \(\hat{n}\) la normal exterior al conductor.

El método que utilizamos para recuperar la Ley de Coulomb puede utilizarse para calcular campos eléctricos en sistemas que presentan un grado de simetría suficientemente grande:

1. Exáminamos las simetrías, y determinamos las posibles componentes no nulas del campo eléctrico.

2. Proponemos una “forma” para el campo eléctrico, en función de algunos parámetros a determinar.

3. Para calcular su valor en un punto, elegimos una superficie gaussiana \({\cal S}\) que pase por el punto, tal que el campo eléctrico sea, o bien 1. normal y constante, o bien 2. paralelo en todos sus puntos.

4. Usamos la ley de Gauss para determinar los parámetros en función de la carga encerrada.

5. Calculamos la carga encerrada por \({\cal S}\) y remplazamos.

Ejemplo 1: Campo por una distribución esférica de carga

Ejemplo 2: Campo generado por un plano cargado

3. Tomamos como superficie gaussiana un cilindro de radio \(a\) y altura \(h\), con el eje perpendicular al plano.
   • El campo es siempre perpendicular a las “tapas” del cilindro, y paralelo a la superficie lateral.
   • La carga encerrada será \(Q=\pi a^2 \sigma\)

Notar que este resultado es consistente con el obtenido para un disco sobre su eje, a una distancia \(z\) mucho menor que su radio \(a\): \[ \vec{E}_{\rm disco}(z\hat{n})=\frac{\sigma}{2 \varepsilon_0 }(1-\frac{z}{\sqrt{z^2+a^2}})\hat{n}\approx \frac{\sigma}{2 \varepsilon_0 }(1-\frac{z}{a})\hat{n}\approx \frac{\sigma}{2 \varepsilon_0 } \hat{n}=\vec{E}_{\rm plano}(z\hat{n}) \]

Ejemplo 3: Campo de una superficie cilíndrica

3. Tomamos como superficie gaussiana un cilindro de radio \(r\) y altura \(h\), concéntrico con el eje de la distribución de carga.
   • El campo es siempre paralelo a las “tapas” del cilindro. Toda la contribución proviene de la superficie lateral.
   • La carga encerrada será \(2 \pi a h \sigma\)

• Ejercicio: ver que el resultado sigue siendo válido para una distribución volumétrica de carga \(\rho(\vec{r})=\rho(r)\) remplazando \(\lambda(r)=2\pi \int_0^r \rho(r^{'}) r^{'} dr^{'}\)

El campo electrostático es Conservativo

• Una forma conveniente de expresar el campo de una carga puntual es en términos del gradiente de una función escalar:

\[ \vec{E}(\vec{r})=\frac{Q}{4\pi\varepsilon_0 |\vec{r}-\vec{r}_0|^2}\frac{\vec{r}-\vec{r}_0}{|\vec{r}-\vec{r}_0|} =-\nabla \frac{Q}{4\pi\varepsilon_0 |\vec{r}-\vec{r}_0|} \] (recordemos que \(\nabla \phi(x,y,z)=\frac{\partial \phi }{\partial x}\hat{x}+\frac{\partial \phi }{\partial y}\hat{y}+\frac{\partial \phi }{\partial z}\hat{z}\) y que \(\nabla \phi(|\vec{r}|)=\phi^{'}(r)\hat{r}\))

• Que un campo vectorial \(\vec{W}\) pueda expresarse como el gradiente de una función escalar \(\phi\) tiene como consecuencia que, para cualquier curva \({\cal C}\) que inicia en el punto \(\vec{r}_i\) y termina en el punto \(\vec{r}_f\) \[ \int_{\cal C}\vec{W}\cdot d\vec{\ell} =\int_{\cal C}-\nabla \phi \cdot d\vec{\ell}=\phi(\vec{r}_i)-\phi(\vec{r}_f) \]
• Además, si \({\cal C}\) es una curva cerrada, \(\oint_{\cal C}\vec{W}\cdot d\vec{\ell} =0\)
• Decimos por lo tanto que tal campo es Conservativo

Partiendo de que el campo electrostático de una carga puntual es conservativo, vemos que (por el principio de superposición lineal) el campo electrostático debido a cualquier distribución de cargas también lo es. De esta manera, \[ \oint_{\cal C} \vec{E}\cdot d\vec{\ell} =0 \] y, para cualquier par de puntos \(\vec{r}_i\) y \(\vec{r}_f\), y curva limitada por estos, \[ \int_{\cal C} \vec{E}\cdot d\vec{\ell} = \int_{\vec{r}_i}^{\vec{r}_f} -\nabla V(\ell) \cdot \vec{ell} =V(\vec{r}_i)- V(\vec{r}_f)= -\Delta V(\vec{r}_f,\vec{r}_i) \]

Llamamos a \(\Delta V(\vec{r}_f,\vec{r}_i)=-\Delta V(\vec{r}_i,\vec{r}_f)\) la diferencia de potencial electrostático entre dichos puntos.

Interpretación física

Supongamos que una partícula de carga \(q\), inicialmente en reposo, es arrastrada a lo largo de una curva \({\cal C}\) en presencia de un campo electrostático, por una fuerza \(\vec{F}\), de forma muy lenta. De esta manera, \(\vec{F}\approx -q\vec{E}\) en cada punto de la trayectoria. El trabajo realizado por la fuerza \(\vec{F}\) es entonces

\[\begin{eqnarray*} W&=&\int_{\cal C}\vec{F}\cdot d\vec{\ell}\\ &=&\int_{\cal C} -q\vec{E}\cdot d\vec{\ell}=q \Delta V(\vec{r}_f,\vec{r}_i) \end{eqnarray*}\]

De esta manera, podemos definir a la diferencia de potencial entre dos puntos \(\vec{r}_f\) y \(\vec{r}_i\) como el trabajo por unidad de carga requerido para llevar una carga de prueba, de forma cuasi-estática, desde el punto \(\vec{r}_i\) hasta el punto \(\vec{r}_f\).

• Identificamos entonces a \(-q\Delta V(\vec{r}_f,\vec{r}_i)\) con el trabajo realizado por el campo eléctrico sobre una carga que se desplaza entre esos puntos.
• En ausencia de otras fuerzas, \(W_{E}=-q\Delta V(\vec{r}_f,\vec{r}_i)\) es igual al cambio en la energía cinética de una partícula al moverse del punto \(\vec{r}_i\) al punto \(\vec{r}_f\).

Unidades y medida de diferencias de potencial

• La unidad de diferencia de potencial en el sistema internacional es el Volt \({\rm V}={\rm Joule}\;{\rm Coulomb}^{-1}\).
• Las diferencias de potencial se miden con instrumentos llamados Voltímetros

El potencial electrostático

En general, dado un punto \(\vec{r}_0\), podemos definir la función \(V_{\vec{r}_0}(\vec{r})=V(\vec{r},\vec{r}_0)\) a la que llamamos potencial electrostático referido a \(\vec{r}_0\).

• La diferencia de potencial entre dos puntos viene dada por \(\Delta V(\vec{r}_f,\vec{r}_i)=V_{\vec{r}_0}(\vec{r}_f)-V_{\vec{r}_0}(\vec{r}_i)\)
• Es fácil ver que la relación entre los potenciales electrostáticos referidos a puntos distintos viene dada por \[ V_{\vec{r}^{'}_0}(\vec{r}_f)=V_{\vec{r}_0}(\vec{r}_f)-V_{\vec{r}_0}(\vec{r}^{'}_0) \]
• Independientemente del referencial elegido, \(\vec{E}(\vec{r})=-\nabla V_{\vec{r}_0}(\vec{r})\)
• El potencial \(V(\vec{r})=V_{\infty}(\vec{r})=\frac{Q}{4\pi\varepsilon_0 |\vec{r}-\vec{r}_0|}\) corresponde al potencial de una carga puntual ubicada en \(\vec{r}_0\) referido a un punto infinitamente lejano.
• Debido a la Ley de Gauss, el potencial electrostático satisface la Ecuación de Poisson: \[ -\nabla^2 V = \nabla \cdot \vec{E} = \rho/\varepsilon_0 \] donde \(\nabla^2\) es el Operador Laplaciano \(\nabla^2 V=\nabla \cdot (\nabla V)\)

Definición

Una superficie equipotencial es el lugar geométrico formado por los puntos del espacio donde el potencial electrostático toma un valor constante.

• Propiedades

  • Son ortogonales al campo electrostático \(\Rightarrow\) son cruzadas ortogonalmente por las líneas de campo electrostático.
  • Toda superficie equipotencial cerrada, encierra una cierta cantidad de carga neta.
  • Alrededor de una carga puntual, tienden a la forma esférica concéntrica a la carga.
  • Para una distribución localizada con carga neta no nula, tienden a una forma esférica para distancias grandes a la distribución.
  • Los conductores definen volumenes equipotenciales: cualquier superficie interior a un conductor es una equipotencial.

Ejemplos

Efecto punta

Conexión a tierra

Energía Electrostática de un sistema de cargas puntuales

Dada una cierta distribución de cargas puntuales \(\{q_i\}\) ubicadas en los puntos \(\vec{r}_i\) podemos calcular el trabajo mínimo necesario para producirla, suponiendo que traemos las cargas que la forman una a una desde el infinito. Este trabajo será la suma de los trabajos \(W_i\) requeridos para traer la partícula i-esima desde infinito hasta su posición. De esta manera la energía potencial electrostática \(U_{pe}\) de un sistema de cargas puntuales viene dada por \[ {U}_{\rm pe} = \sum_i W_i \] \[ W_i=q_i V_i(\vec{r}_i)\;\;\;\;\; V_i(\vec{r}_i)=\sum_{j<i} \frac{q_j}{4\pi\varepsilon_0 |\vec{r}_i-\vec{r}_j|} \] Luego, \[ {U}_{\rm pe}=\frac{1}{2}\sum_{j\neq i} \frac{q_i q_j}{4\pi\varepsilon_0 |\vec{r}_i-\vec{r}_j|} \]

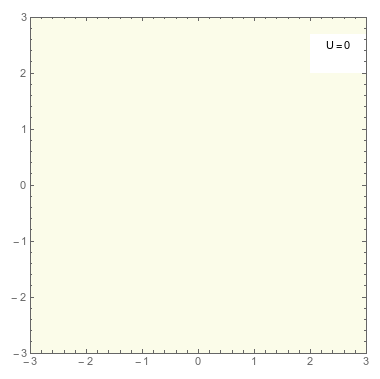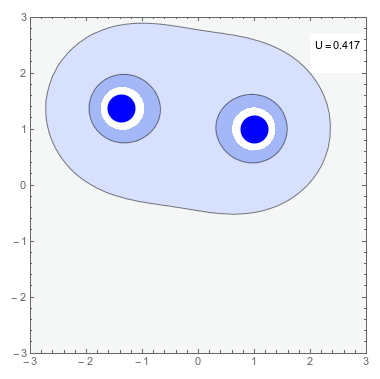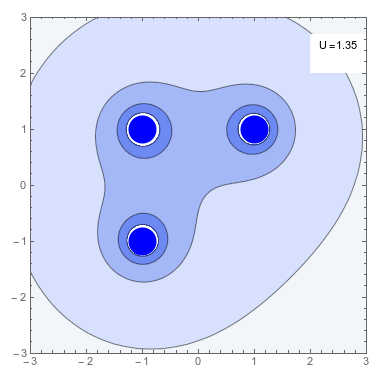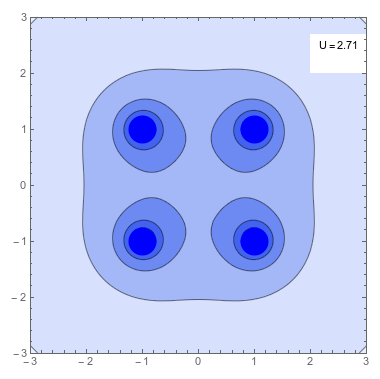
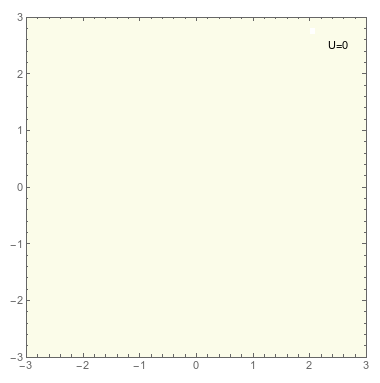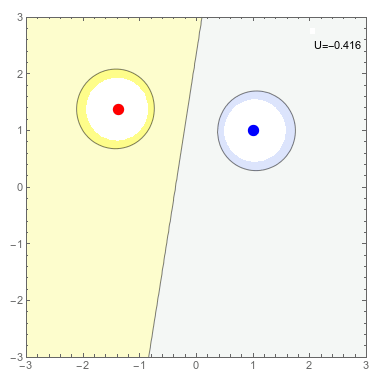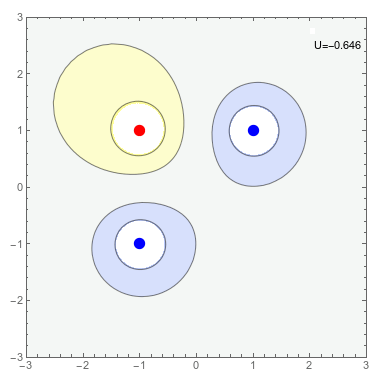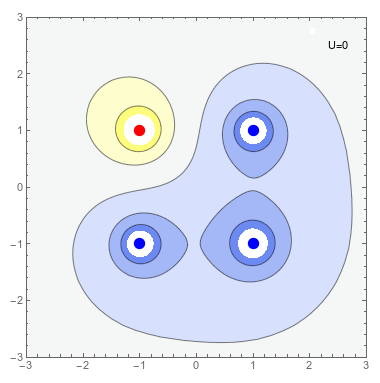
Densidad de Energía Electrostática

En general, para distribuciones continuas de carga, se puede mostrar que \[\begin{eqnarray*} U_{\rm pe}&=&\int \frac{\varepsilon_0|\vec{E}(\vec{r})|^2}{2} d^3r\\ \end{eqnarray*}\] Por este motivo, se suele denominar a \({\cal E}=\frac{\varepsilon_0|\vec{E}(\vec{r})|^2}{2}\) la densidad de energía electrostática.